WOODEN POLYHEDRA 30
正多面体５種類、準正多面体１６種類、準正多面体の双対６種類と、平行多面体から六角柱・長菱形１２面体、
に切稜立方体を加えた木製多面体のセットです。
fig.1
fig.2
fig.3
fig.4
fig.5
fig.6
fig.7
fig.8
fig.9
fig.10
fig.11
fig.12
fig.13
fig.14
fig.15
fig.16
fig.17
fig.18
fig.19
fig.20
fig.21
fig.22
fig.23
fig.24
fig.25
fig.26
fig.27
fig.28
切稜立方体は立方体からさまざまな多面体を木工製作するさいに、しばしば原型となる立体です。
(The chamfered cube often appears to be a prototype in the hand-made modelling from the wooden cube to various polyhedra.)
(The chamfered cube often appears to be a prototype in the hand-made modelling from the wooden cube to various polyhedra.)
Wooden solid wonder-world of Hiroshi NAKAGAWA
Ikuro SATO
Hiroshi NAKAGAWA is a special carpenter skillful for making polyhedra of wood. He planned to make polyhedron concrete so that students can begin to understand and appreciate mathematics.
The wooden polyhedra are composed of 30 pieces shown in figures, including 5 Platonic(Fig 1-5), 16 Archimedean(Fig 6-19), 6 Catalan(Fig 20-25), 2 Fedrov(Fig 26-27) and the chamfered cube(Fig 28).
About the chamfered cube(Fig 28), this is the most favorite solid of him, because the chamfered cube often appears to be a prototype in the hand-made modeling from the wood cube to various polyhedra.
He hopes and believes that the wooden polyhedra are useful for the students to entertain, inform and teach some mathematics. But, his interest is not limited in hand-made modeling of wooden polyhedra. He is interested in surprisingly wide topics. Especially, I want to introduce a recent episode of the collaborative study of NAKAGAWA and J. AKIYAMA.
In June 2008 an international congress was held in Moscow for celebrating the 100 years anniversary of birth of the Russian mathematician L. S. Pontrjagin. In this congress a Japanese mathematician J. Akiyama made a lecture on the set and the element number of parallelohedra, "New theorem about parallelohedra".
Fedorov's parallelopolyhedra are defined as polyhedra with the following conditions:
a. each face has a parallel counterpart,
b. each edge belong to a group of parallel edges,
c. repetition of the same polyhedra must fill the space to produce a translation symmetry only (neither rotation nor reflection).
These polyhedra are limited to the five members consisting of cube(Fig 2), truncated octahedron(Fig 8), rhombic dodecahedron(Fig 24), hexagonal prism(Fig 26) and elongated rhombic dodecahedron(Fig 27). These polyhedra are less popular than the Platonic bodies, but are considered equally important because they play a role of space packing.
Now, let us consider the problem "what is a space-tessellation producer?", i.e. what is an elementary body producing space filling bodies?". General proof of this problem is quite difficult, but simple examples are found as follows.
We can construct all of the parallelopolyhedra with one kind of element, where its mirror image is looked upon as the same one. Let the element be denoted by σ, then the cube is constructed by 96 elements of one kind (σ96), the hexagonal prism is σ144, the rhombic dodecahedron is σ192, the elongated rhombic dodecahedron is σ384 and the truncated octahedron is σ48.
fig.29
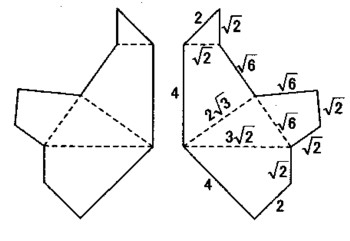fig.30
Fig.29 The pentahedron σ is an atom building up all of the 5 types of Fedorov's polyhedra, whose development is shown in Fig.30.
November 1,2013
各種多面体のご注文、お問い合わせはこちらへどうぞ
ご予算におうじて製作いたします。お気軽にご相談ください。
Payment: 'Paypal',etc.
For inquiry or order
fig.29fig.30Fig.29 The pentahedron σ is an atom building up all of the 5 types of Fedorov's polyhedra, whose development is shown in Fig.30.
November 1,2013
各種多面体のご注文、お問い合わせはこちらへどうぞ
ご予算におうじて製作いたします。お気軽にご相談ください。
Payment: 'Paypal',etc.
For inquiry or order
ご予算におうじて製作いたします。お気軽にご相談ください。
Payment: 'Paypal',etc.
For inquiry or order